Tranh cãi bài hình học lớp 5 thử thách tư duy nhanh

Một hình ngũ giác được cho như hình vẽ sau: 

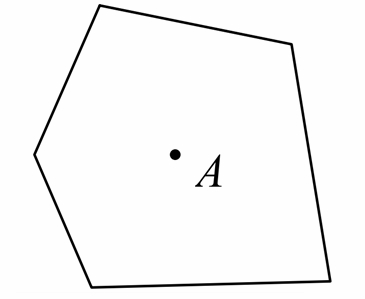
Diện tích hình ngũ giác là 20 cm2. Điểm A nằm ở trong ngũ giác và cách đều tất cả các cạnh của ngũ giác một khoảng bằng 5 cm.

Hỏi chu vi ngũ giác bằng bao nhiêu?

Một bạn đọc phân tích: Gọi hình ngũ giác là BCDEF với A cách đều các cạnh 5cm. Diện tích ngũ giác = DT 5 tam giác (ABC, ACD, ADE, AEF, AFB)=1/2* 5*(BC+CD+DE+EF+FB) (vì A cách đều 5 cạnh 5cm nên A...là đường cao của các tam giác) = 20cm2=> Chu vi ngũ giác = 8cm.

Một bạn đọc cũng tính toán: Đặt tên các đỉnh ngũ giác lần lượt là B, C, D, E, F. Diện tích ngũ giác bằng tổng diện tích các tam giác ABC, ACD, ADE, AEF, AFB-> 20 = 1/2 * (BC + CD + DE + EF + FB) * 5-> Chu vi ngũ giác = 8.

Tuy nhiên, bạn đọc khác lại cho rằng, không tồn tại. Với bán kính 5cm, chúng ta có thể vẽ 1 hình tròn đi qua 5 điểm tiếp xúc từ A đến các cạnh ngũ giác, lúc này chu vi hình tròn sẽ nằm trong chu vi hình ngũ giác. Các bạn tính ra được chu vi hình ngũ giác là 8cm. Nhưng chu vi hình tròn là dxpi=2x5x3,14=31,4cm.=> Với dữ liệu trên thì không thể tồn tại chu vi ngũ giác 8cm.

Cũng có bạn đọc cho rằng, đề ra sai. Với dữ kiện đã cho chỉ có thể vẽ thành hình chóp ngũ giác và diện tích 20cm2 là diện tích 5 mặt bên của hình chóp, chỉ vì 20cm là chu vi đáy hình chóp.

Đồng tình, một bạn đọc viết: Tính đáp số thì dễ nhưng có vẻ thực tế không tồn tại hình nào như vậy, đố ai vẽ được hình như thế...

Bạn đọc có thể tiếp tục đưa ra ý kiến của mình.